a modular Mandelbulb
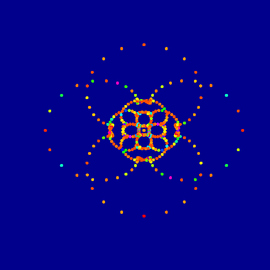
A piece from the geometric view. A modular power 8 Mandelbulb consisting of 3 power 2 Mandelbulbs. Just a gimmick but with some nice features. And - just to mention - this system has eluded algebraists for 15 years.
I must admit, that I do not fully understand, why this system works. It was a shot in the dark, based on a vague idea, that turned out to be true.
The formula coders of the Mandelbulber team have noticed that system, so I am courious, what they come up wirth.
After starting with the default, power flexible Mandelbulb, it turned out, that the most simple Mandelbulb - power 2 is suitable as single module. As trigonometry is involved, a certain system does not nessecariely need to be unique in geometric coming out. In experimental evidence, the power 2 Mandelbulb is geometrically identical (in single formula and modular use) to the default, power flexible Mandelbulb in power 2 and with alpha and beta offset is set to 90°. We maybe have a problem here, to define formal descriptions clear and unique.
In Mandelbulb 3d I can’t implement that system, because I can’t hinder a module to add global c. But the solo module can be built.
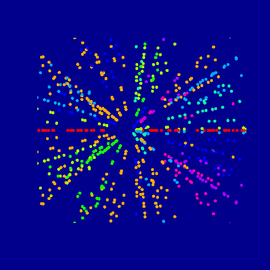
The M-set
The objective is simple. We build a power 8 Mandelbulb from three superimposed power two Mandelbulbs. In Mandelbulber 2 the most simple implementation of a power 2 Mandelbulb is used as only module. Global c is added one time after the third power 2 Mandelbulb. Result is something very similar to a power 8 Mandelbulb.
>>parameters are still the initial approach and will be replaced as soon as possible.
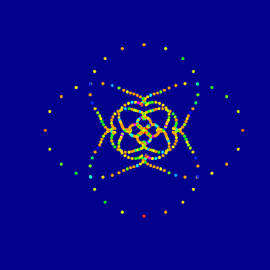
top view
Similar we can say, because it has defined properties, that match the expectations of a power 8 Mandelbulb.
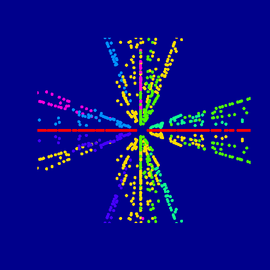
Mandelbulbs of power n have in top view n-1 “antennas”. Remember: The 2-dimensional Mandelbrot set has n-1=2-1=1 antenna. The modular Mandelbulb has seven antennas. That’s why we can be sure, that this is really similar to a power 8 Mandelbulb.
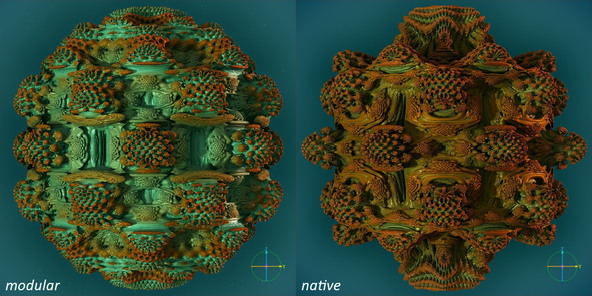
modular and native
Similar but not equal we must say, because the native power 8 Mandelbulb of the same formula base looks sightly different than the modular construction.
The parameter is somewhat optimized, so you can change between modular and native display with just a few clicks.
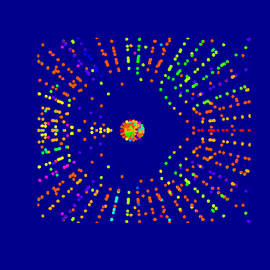
the module
There are several ways, to define modules. I started with the Mandelbulber default Mandelbulb, But one of the most simple implementations of a power 2 Mandelbulb does it as well.
http://www. fractalforums.com/3d-fractal-generation/true-3d-mandlebrot-ty…
power shifting
Based on a suggestion by Graeme McLaren - aka Carbuncle Grim
By altering the power of Mandelbulb#1 you can change the power of the whole Mandelbulb. Some examples.
power 2.25, power2, power 2 creates a
power (2,25*2*2) = power 9 Mandelbulb (counting n-1 in top view)
power 3, power 2, power 2 creates a
power (3*2*2) = power 12 Mandelbulb
So at this point is at least clear that it is a plain multiplication until c is added.
Image shows the power 9 modular Bulb.
>p 2 do
ortho plantage
As an artist, my first interest is of course the artistic quality, the possibility of making something unique out of it. And the first thing that came to my mind was adding c in different places. Here c is added after the first slot and not the third. Result is a shape, quite unique for Mandelbulbs. And as the distance between two add c operations stays three slots, the “bulbish” character of the shape remains intact.
