Difference bracelets
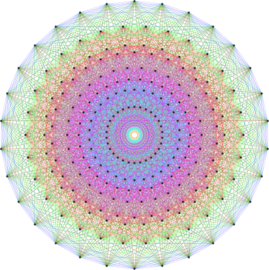
A difference bracelet consists of v beads. There are k beads of n colours and one black bead (v = k n + 1). The beads are arranged so that there are exactly λ equally coloured beads at each possible distance for every colour. The distance of a pair of beads is the number of moves to get from one to the other, either clockwise or counter-clockwise (every pair of beads has two distances). Such an arrangement is called a (v,k, λ) bracelet. The number of colours can be computed as n = v / (k - 1). The gallery contains pictures of bracelets with parameters (7,3,1), (11,5,2), (19,9,4), (31,6,1), (37,9,2), and (73,9,1).
The beads of any single colour represent a (v,k, λ) difference set in the cyclic group of order v. The black bead is the identity element. Bracelets are in fact tilings of cyclic groups with difference sets. The concept has been defined and studied in the paper A.Ćustić, V.Krčadinac, Y.Zhou, Tiling Groups with Difference Sets, Electronic Journal of Combinatorics 22 (2015) #P2.56.

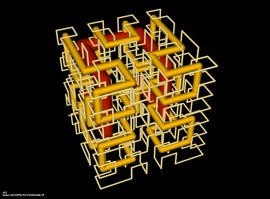
A (31,6,1) bracelet
The bracelet consists of 6 beads in each of 5 colours and a black bead. For every colour and every distance from 1 to 30, there is exactly one pair of beads in the specified colour at the specified distance. The colours define (31,6,1) cyclic difference sets giving rise to projective planes of order 5.

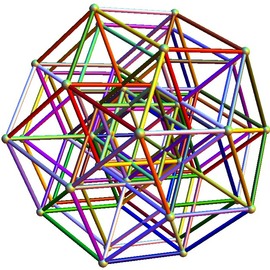
A model of the (31,6,1) bracelet
Difference bracelets cannot be built without the black bead, representing the identity element of the group. A slightly larger faceted bead was used here.

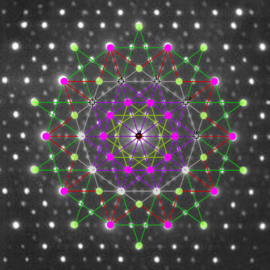
A (37,9,2) bracelet
The red beads in this (37,9,2) bracelet correspond to the fourth powers in the field of order 37. This is a multiplicative subgroup, and the other colours correspond to its cosets.

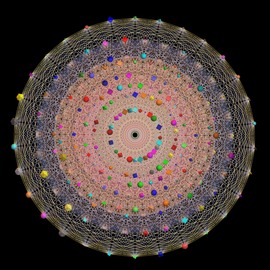
A (73,9,1) bracelet
This large bracelet or necklace was constructed from the eighth powers in the field of order 73. The colours represent (73,9,1) cyclic difference sets, giving rise to projective planes of order 8.
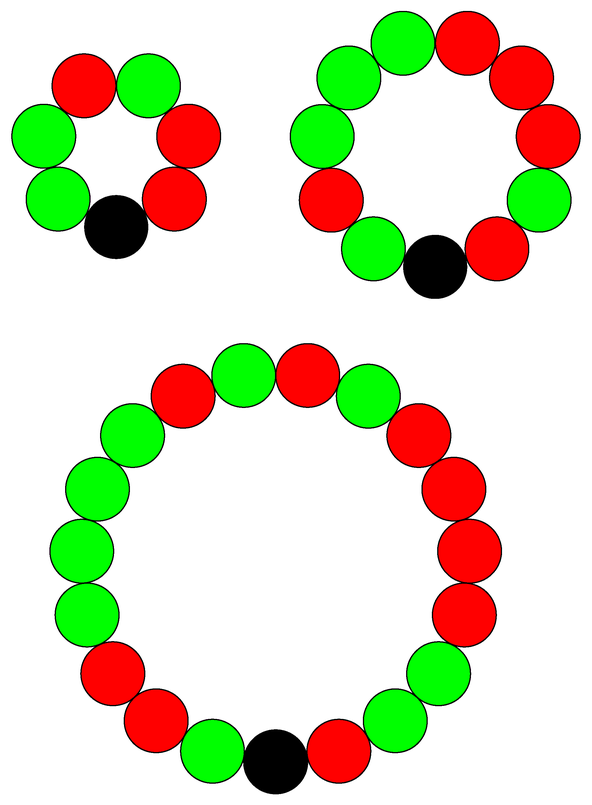
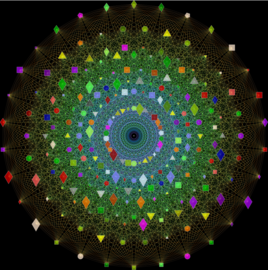
Bracelets of two colours
Bracelets of two colours can be built whenever v is a prime congruent to 3 modulo 4. The picture shows (7,3,1), (11,5,2) and (19,9,4) bracelets. Red corresponds to the squares and green to the non-squares in the field of order v.