The Heidelberg Laureate Forum Foundation invites you to visit the exhibition “Mathematics of Planet Earth” at Karlstorbahnhof in Heidelberg, Germany! It runs from July 5 to Aug 2, 2015, for the first time in Heidelberg. It offers a big variety of exciting adventures for children and adults alike.
Embaldosados cuasicristalinos
In 1982, Dan Shechtman descubrió una estructura nuclear con un conjunto de cinco simetrías rotacionales. Hoy en día, las estructuras nucleares de este tipo se denominan cuasicristales.
En general, los patrones de crecimiento para cuasicristales decagonales con un conjunto de diez o cinco simetrías rotacionales se basan en las teselaciones geométricas y cuasiperiódicas descubiertas por Roger Penrose en 1973.

Embaldosados cuasicristalinos
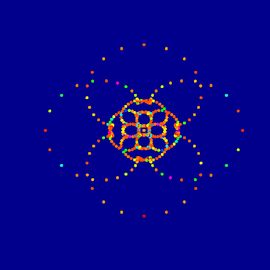
Las decoraciones de embaldosado, en primer plano de los gráficos de gran tamaño, corresponden a la estructura de los cuasicristales, aunque sus patrones ya habían diseñados como azulejos girih por los artesanos medievales (los nudos girih persas).
Al insertar las plantillas girih en una teselación de penrose romboide moderna, se creó un tejedo de mimbres girih con una simetría rotacional casi perfecta diez. Los nodos cerrados resultantes (verde, amarillo y azul) sorprendentemente corresponden a la geometría de un modelo de cubierta comúnmente utilizado hoy en día, que se puede ver en el fondo de la mimbre.
Una descripción detallada se puede encontrar en documentos como los que se muestran debajo o debajo de la imagen.
Esta imagen, así como algunas otras de esta galería, forman parte de la exposición «IMAGINARY - Form und Formel mathematischer Fantasie», que se mostró por primera vez en junio de 2016 en Nuremberg.
(www. imaginary.org/event/imaginary-in-nuremberg)
(www. imaginary.org/event/imaginary-at-sigena-gymnasium-in-nuremberg)
(www. imaginary.org/gallery/hand-made-hands-on)
(https://patterninislamicart.com/s/collections/main-archive/piia_image/tu…) Girih pattern in Kayseri
La profesora de geometría aperiódica
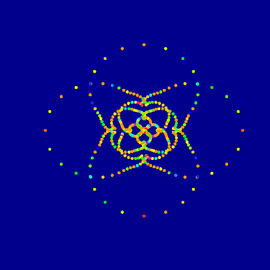
La estructura subyacente de esta imagen es la de un teselación rómbico de Penrose cuasiperiódico (aperiódico), uno de los modelos geométricos que se utilizan para los cuasicristales decagonales. La forma del área amarilla tiene una simetría rotativa décuple, aunque su centro es asimétrico. Los arreglos de este tipo se llaman diseños de ruedas de carro (en. cartwheel)
La profesora demuestra en 35 posiciones diferentes lo que significa golpear una rueda. Reduce la simetría rotacional décuple a una simetría rotacional quíntuple dándonos la espalda 15 veces y alude al orden de una teselación de Penrose romboédrica espacial.
Sugerimos comparar con la capitulo III del folleto descriptivo.
Los objetos prácticos que ilustran un algoritmo de crecimiento (Sucesión cuasiperiódica, capítulo V) con el que se puede construir sucesivamente una estructura de rueda de carro impecable se pueden encontrar en la segunda mitad de la galería Hecho a mano.
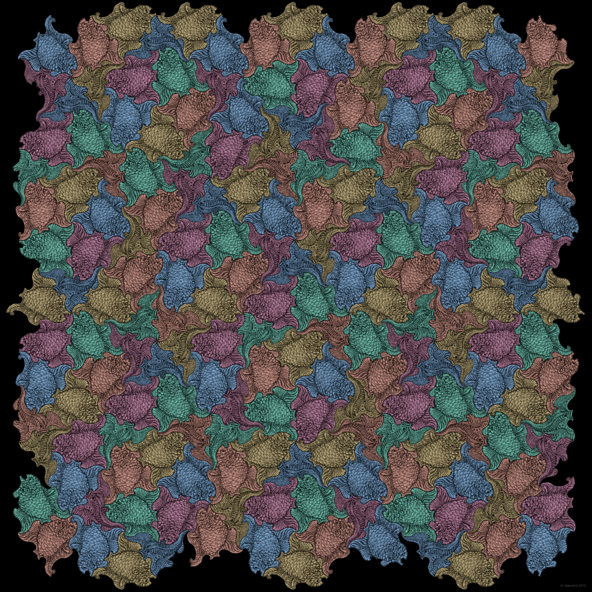
Cuasiperiodicidad animal
La imagen adyacente se inspiró en el famoso trabajo del conocido artista holandés MC Escher, quien unió sus figuras de una manera igualmente impecable.
Los principios de disposición de Escher eran periódicos con una correspondencia con el orden atómico de los cristales. En contraste, la imagen que se presenta aquí se basa en una teselación de Penrose cuasiperiódica y, por lo tanto, corresponde a un orden atómico cuasicristalino con una simetría rotacional quíntuple que no puede ser cristalográfica.
Los peces rojos nadan en cinco orientaciones diferentes, cada una girada 36 grados entre sí.
La coloración turquesa nos permite detectar la forma del cubo de una rueda de carro.
Estructura de teselatión animal
Esta imagen demuestra la relacion de los animales ordenados cuasiperiódicamente a cuatro teselaciones diferentes pero mutuamente derivables.
El área en forma de anillo consiste en triángulos amarillos y naranjas, los llamados triángulos de Robinson. Dentro del anillo, los triángulos se combinan en romboides Penrose azules gruesos y verdes delgados, en el exterior en kites azules y flechas verdes.
Todos los kites tienen un equivalente uno a uno con un pentágono Penrose azul, verde o amarillo en el fondo. La esquina cóncava de una flecha siempre está en medio de un pentágono negro, la punta de flecha en medio de uno púrpura. Los puntos blancos y negros representan las reglas de teselación de kites y flechas.
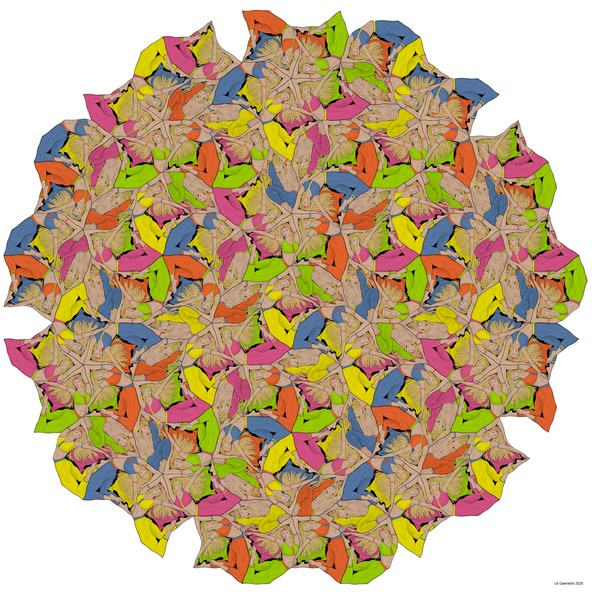
Rotación quíntuple animal
En una estructura atómica cuasicristalina, para la cual se puede detectar una simetría quíntuple, los centros de simetría deben distribuirse uniformemente en toda la estructura y deben existir centros con diferentes rangos.
¡Los modelos cuasiperiódicos optimizados, como el teselaciones Penrose, son sistemas jerárquicos!
En el ejemplo estructural adyacente ilustrado animalísticamente, se destacan 13 centros de turquesa de simetría quíntuple. Los 10 centros en el borde de la imagen están ubicados exactamente en las esquinas de un decágono. Las direcciones de rotación de los centros de simetría se alternan consistentemente.
Donde cinco de las «tortugas» de color ocre juntan sus cabezas, hay centros de simetria quintuple con rangos más largos.
Girih Cartwheel
Este ornamento girih estaba compuesto por solo dos azulejos de girih diferentes, hexágonos irregulares y trapecios.
Las reglas de creación aperiódica de bloques de construcción están definidas por seis colores diferentes en sus áreas de esquina. Por favor, compare el archivo de rompecabezas Girih Tiling debajo de la imagen.
Dentro del decágono con centro C y vértice superior T, las superficies de las esquinas del mismo color se ensamblaron en pentágonos y pentágonos dobles de tal manera que corresponden a una rueda de carro de Penrose.
La extensión de esta estructura a toda el área de la imagen fue creada por cuatro superposiciones con copias de la rueda de carro central. Los rombos PLVR muestran la ubicación de las cinco ruedas de carro.
Si una forma pentagonal roja, azul o amarilla se refleja en una de las líneas negras radiales, entonces su reflejo es verde, naranja o púrpura.
Golden Girih Cartwheel Relievo
El trabajo de relieve adyacente es una versión editada digitalmente del gráfico anterior titulado «Girih Cartwheel».
El método de procesamiento desarrollado por el fotógrafo de Nuremberg Thomas Bischof se aplicó globalmente a toda la imagen, sin ninguna intervención separada en los detalles de la imagen.
Se pueden descargar dos archivos png de alta resolución de dos versiones de relieve diferentes.
Están sujetos a la misma licencia abierta que los demás gráficos de la Galería Wickerwork, es decir, pueden mostrarse en todos los contextos no comerciales, cuidando la mejor calidad de imagen posible y la preservación del formato original.

Mimbre octogonal
Las primeras estructuras atómicas con simetría rotacional de ocho veces fueron descubiertas en 1987. Estas estructuras son cuasicristalinas, ya que un orden cristalino (periódico) puede tener como máximo una simetría rotacional de tres, cuatro o seis veces.
Una descripción geométrica es hecha por el parquet Ammann-Beenker. Sus bloques de construcción son cuadrados o rombos con ángulos de 45 °. La combinación de los bloques de construcción más pequeños en bloques de construcción más grandes y visibles en color muestra el carácter jerárquico de la estructura. El patrón de cesta dibujada tiene una referencia directa a los bloques de construcción de ambos tamaños.
El área octogonal iluminada en el centro de la imagen, que contiene dos grandes cuadrados y cuatro grandes diamantes, corresponde a uno de los octágonos de Gähler, con los que el área se puede cubrir completamente (con superposiciones) y que están en proporción uno a uno a los anillos brillantes cerrados.
Color-Coded Kites and Darts
El parqué de Penrose que se muestra aquí se conoce como kites y flechas. Su simetría rotacional décuple es detectable en cuasicristales decagonales.
Un papel a cuadros tiene una simetría rotacional de orden cuatro, es decir, el papel ofrece la misma vista nuevamente después de una rotación de 90 ° alrededor de un punto libremente seleccionable. Sin embargo, a diferencia del papel a cuadros, el parquet Penrose no tiene una estructura periódica. Aunque sus bloques de construcción solo se combinan parcialmente para formar estrellas o decágonos rotacionalmente simétricos, el parquet no cambia fundamentalmente después de una rotación de 36 °, ya que los kites y las flechas están nuevamente presentes en números iguales en las diez orientaciones posibles después de la rotación.
La coloración uniforme de los bloques de construcción con una cierta orientación hace que las secuencias cuasiperiódicas con el cambio característico y no periódico de distancias sean claramente visibles.
Compare el archivo con la secuencia de imágenes directamente debajo del gráfico.
Kite Fish & Dart Rays
Las figuras de este cuadro están compuestas a la manera del artista M. C. Escher, pero no poseen el orden periódico característico de su obra gráfica. La disposición de los peces y las rayas se ha tomado de la imagen anterior, un parquet Penrose cuasi-periódico y geométrico.
Las esquinas de las figuras corresponden a las esquinas del parquet geométrico, pero los bordes rectos de los bloques de construcción geométricos se deforman en contornos en los bloques de construcción figurativos.
Mientras que los bloques de construcción geométricos también permiten composiciones periódicas, la yuxtaposición de peces y rayas fuerza un orden cuasi-periódico.
Dos bloques de construcción geométricos del mismo tipo, girados 36 ° entre sí, tienen su contraparte en figuras de espejo invertidas.