The first MPE2013 exhibition featuring the winner modules of the MPE2013 competition held in collaboration with IMAGINARY takes place from March 5 – 8, 2013 at the UNESCO headquarters in Paris.
Quasicrystalline Wickerwork
1982년 D. Shechtman은 5중 회전대칭을 이루고 있는 핵심 구조를 발견했습니다. 오늘날 이런 형태의 핵심 구조들은 준결정(Quasicrystal)이라 불립니다.
일반적으로 10 개 또는 5 개의 회전 대칭을 형성하는 십각형 준 결정의 성장 모델은 1973 년 Roger Penrose가 발견 한 준주기 기하학적 쪽모이 세공을 기반으로합니다.

Quasicrystalline Wickerwork
이 대형 그림 전면의 바자얽기(wickerwork) 모양 장식은 중세의 기리(girih, 역주: 이슬람 건축의 장식에 사용되던 타일, 페르시아어로 ‘매듭’이라는 뜻) 타일에서 디자인을 따 왔지만, 이는 사실 십각형 준결정의 단위구조와 정확히 일치합니다.
이 매듭 타일을 최신 마름모꼴 Penrose 타일에 적용하면 10 개의 회전 대칭이있는 패턴을 만들 수 있습니다. 그 결과 닫힌 노드(녹색, 노란색 및 파란색)는 놀랍게도 오늘날의 커버 모델의 지오메트리와 일치합니다. 지오메트리는 바스켓 메쉬의 배경에서 볼 수 있습니다.
이 이미지에 대한 자세한 설명은 아래 설명(독일어/영어) 또는 그래픽 바로 아래의 이미지 시퀀스에서 찾을 수 있습니다.
이 갤러리의이 그래픽 및 기타 그래픽은 “IMAGINARY - Form und Formel mathematischer Fantasie” 전시회의 일부입니다. 이 전시회는 2016 년 6 월 뉘른베르크에서 처음 선보였습니다.
(www. imaginary.org/event/imaginary-in-nuremberg)
(www. imaginary.org/event/imaginary-at-sigena-gymnasium-in-nuremberg)
(www. imaginary.org/gallery/hand-made-hands-on)
(https://patterninislamicart.com/s/collections/main-archive/piia_image/tu…) Girih pattern in Kayseri
Woman Teaching Aperiodic Geometry
이 그림의 근본적인 구조는 준(準)주기 (또는 비(非)주기) 마름모꼴 펜로즈 타일링입니다. 이는 십각형의 준결정(quasicrystal)을 모델링할 때 쓰이는 기하학적 구조입니다.
이 그림의 중심부는 비대칭적이지만, 노란색으로 채색되어 있는 영역의 모양은 10중의 회전 대칭성을 보여줍니다. 이 배열은 수레바퀴(cartwheel)라 불립니다.
서로 다른 35개의 위치를 취함으로써, 젊은 여자는 회전 재주넘기(cartwheel, 역주: ‘수레바퀴’와 ‘재주넘기’의 두 가지 뜻이 있음)하는 모습을 보여줍니다. 마름모꼴 펜로즈 타일링의 어려운 배열을 통해 여자는 15바퀴를 돌고 있습니다.
아래 pdf 파일로 제공되는 소개 책자(Description Booklet, 영어/독일어)의 III장과 비교해 보세요.
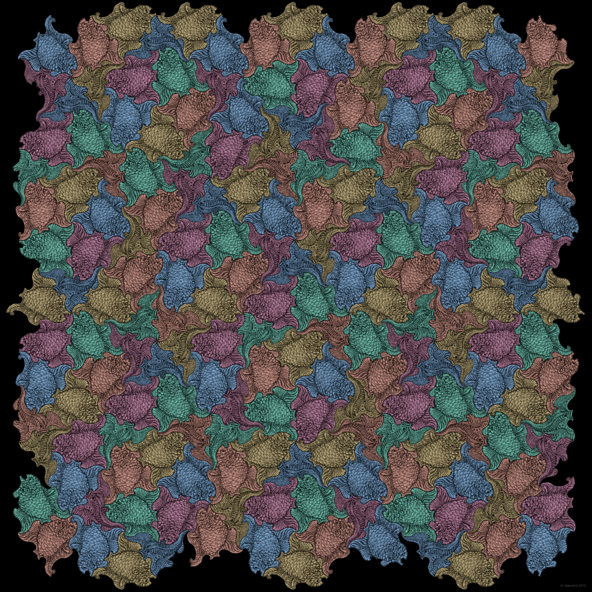
Animalistic Quasiperiodicity
지금 보시는 이 그림은, 세계적으로 이런 형태의 디자인으로 유명한 네덜란드의 예술가 M. C. Escher의 작품들에서 영감을 받아 만들어진 그림입니다.
Escher의 배열은 주기적이며 결정의 단위구조와 일치합니다. 그러나 이 그림은 준주기적인 펜로즈 타일링을 바탕으로 만들어 졌으며, 5중 회전 대칭의 준결정 단위구조와 일치합니다.
빨간색으로 칠해진 물고기들은 5개의 다른 방향으로 헤엄치고 있으며 사잇각은 36도를 이루고 있습니다.
옥색의 물고기들이 수레바퀴(cartwheel)의 중심모양을 찾을 수 있게 도와줍니다.
Animalistic Tiling Structure
이 그림은 준결정 형태로 배치된 4마리 동물과, 서로 다르지만 연관되어 있는 4가지 타일링들의 대응관계를 보여줍니다.
반지 형태의 구역은 노란색과 주황색의 ‘Robinson 삼각형’들로 구성되어있습니다.
반지의 내부에 있는 삼각형들은 두꺼운 파란색과 작은 초록색의 펜로즈 마름모를 이루고 있으며, 반지의 바깥은 파란색 연과 초록색 다트 모양을 이루고 있습니다.
그림 속 마름모는 배경의 펜로즈 타일링을 이루고 있는 파란색 오각형들과 일대일 대응이 됩니다.
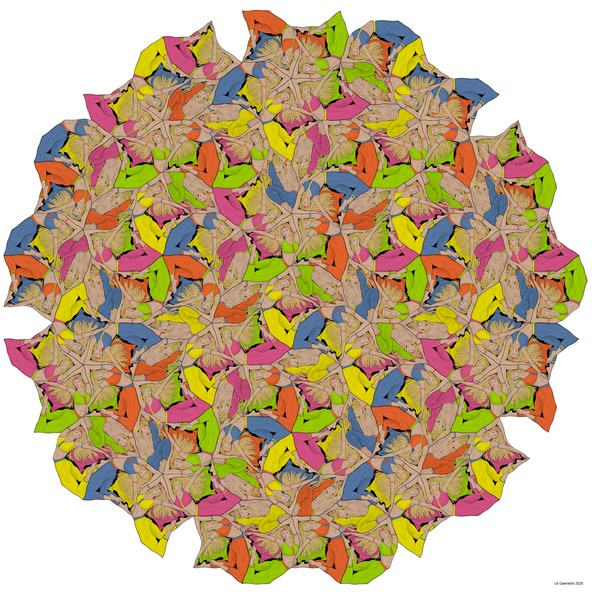
Animalistic Fivefold Rotation
5중 회전 대칭을 갖는 준주기 핵결합 구조를 달성하려면 여러 회전 대칭 중심이 구조 전체에 고르게 분포되어야 하며 범위가 다양한 여러 회전 대칭 중심이 있어야 합니다.
Penrose 타일과 같이 준 주기성을 가진 최적화 된 모델에는 계층 적 시스템이 있습니다.
이 그림에서는 5 배 회전 대칭을 형성하는 13 개의 중심이 옥으로 칠해져 있습니다. 가장자리에 분포 된 10 개의 중심은 정확히 데카곤의 모서리에 있습니다. 회전 대칭의 회전 방향은 규칙적으로 번갈아 가며 나타납니다.
5 개의 주황색 “거북이”의 머리가 수집되는 곳에는 더 넓은 범위의 회전 대칭의 3 개의 중심이 있습니다.
Girih Cartwheel
이 바자얽기 장식은 육각형과 사다리꼴의 매듭 형태 만으로 이루어져 있습니다. 구석의 6가지 다른 색들이 이들의 비주기적인 배열규칙을 정의합니다 (Please compare the file Girih Tiling Puzzle provided below the image).
중심이 C이고 윗 꼭지점이 T인 십각형 내부에서, 같은 색의 꼭지점 구역에서는 오각형과 쌍둥이 오각형(역주: 오각형 둘이 붙어 있는 모양)을 구성하고 있습니다. 이들은 서로 펜로즈의 수레바퀴(Penrose cartwheel) 체계에 대한 동치관계를 이루고 있습니다.
이 그림의 전체 형태는 중심의 수레바퀴를 4번 겹쳐서 만들었습니다. 마름모 PLVR이 이 5개의 바퀴들의 위치를 보여줍니다.
빨강, 파랑 혹은 노랑색으로 이루어진 오각형이나 쌍둥이 오각형을 검정색 선에 반사시키면, 초록, 주황 혹은 보라색으로 되어 있는 거울대칭상을 볼 수 있습니다.
Golden Girih Cartwheel Relievo
표시된 부조는 이전 그래픽의 디지털 편집 버전 인 소위 “Girih 왜건 휠”입니다.
뉘른베르크 사진 작가 Thomas Bischof가 개발 한 처리 방법은 이미지 세부 사항에 대한 별도의 개입없이 전체 이미지에 전체적으로 적용되었습니다.
두 가지 다른 릴리프 버전의 두 개의 고해상도 png 파일을 다운로드할 수 있습니다. Wickerwork 갤러리의 다른 그래픽과 동일한 오픈 라이선스가 적용되며, 즉, 가능한 최상의 이미지 품질과 원본 형식의 보존을 고려하여 모든 비상업적 맥락에서 표시될 수 있습니다.

Octagonal Wickerwork
8중 회전 대칭의 처음 핵심 구조는 1987년에 발견되겠습니다. 주기적인 결정 격자느 3, 4, 6중 회전만을 가져야 하므로, 이 구조는 준주기적이 됩니다.
Ammann-Beenker 타일링을 이용하여 이 구조를 기하학적으로 묘사할 수 있습니다. 타일은 정사각형과 사잇각이 45도인 마름모 두 가지로 이루어집니다. 그림의 배색에서 관찰되는 작은 타일로 큰 타일을 조합하는 방식은, 이 구조의 계층성을 잘 보여줍니다. 그려진 바자얽기 장식은 어떤 스케일에서건 타일들과 명확한 연관성을 갖습니다.
그림 중간에는 두 큰 사각형과 두 큰 마름모가 있는 부분이 강조되어 있고, 이는 Gähler 팔각형이라 불리는 대상과 대응됩니다. 이 팔각형들은 평면을 겹치면서 완전히 덮고, 바자얽기 장식의 하나하나의 닫힌 고리들과 대응됩니다.
Color-Coded Kites and Darts
여기에 표시된 Penrose 쪽모이 세공은 연 & 다트로 알려져 있습니다. 그것의 10 배 회전 대칭은 십각형 준 결정에서 감지 할 수 있습니다.
체크 무늬 용지에서 차수 4의 회전 대칭이 완벽하게 실현됩니다 (즉, 자유롭게 선택한 점을 중심으로 90 ° 회전하면 패턴이 변경되지 않은 것처럼 보입니다). 체크 무늬 종이와 달리 Penrose 쪽모이 세공에는 주기성이 없습니다. 빌딩 블록이 부분적으로만 모여 회전 대칭 별 또는 십각형 모양을 형성하지만, 용과 화살이 가능한 10가지 방향 모두에서 똑같이 자주 나타나기 때문에 쪽모이 세공 패턴은 36° 회전 후에도 본질적으로 변경되지 않습니다.
특정 방향을 가진 빌딩 블록의 균일 한 채색은 특성적이고 비주기적인 거리 변화가있는 준주기적 시퀀스를 명확하게 볼 수있게합니다.
그래픽 바로 아래에 이미지 시퀀스가 있는 파일을 참고하십시오.
Kite Fish & Dart Rays
이 그림의 인물은 예술가 M. C. Escher의 방식으로 구성되었지만 그의 그래픽 작품의주기성의 특징은 없습니다. 물고기와 광선의 배열은 준 주기적 기하학적 Penrose 쪽모이 세공을 보여주는 이전 그래픽과 일치합니다.
각 그림의 모서리는 기하학적 쪽모이 세공의 빌딩 블록의 모서리에 해당하지만 기하학적 빌딩 블록의 직선 모서리는 비 유적 빌딩 블록의 윤곽으로 변환됩니다.
기하학적 빌딩 블록은 또한 주기적인 건설을 허용하지만 물고기와 광선의 구성은 준주기적인 순서를 강요합니다.
동일한 유형의 두 기하학적 빌딩 블록이 서로 36° 회전하면 해당 비 유적 블록은 거울 이미지입니다.