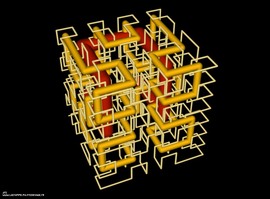
Some 2D Math Pictures
Christian Gaier creates colorful geometric-mathematical pictures and videos as hobby. He developed a set of mathematical functions to visualize basic geometric objects (line, circle and arc) in a surrounding colorful field. These functions can be easily combined to create more complex geometric structures. The main idea is that these functions deliver zero values at the position of the geometric object. Therefore, combinations of these functions can be easily realized by simple multiplications. The software units for picture computation are written in the programming language C.
Links to related videos:
https://youtu.be/VJpJMtZUMVo
https://youtu.be/wBKSmwOt1Q8
https://youtu.be/oP1YrE7E-DU
https://youtu.be/d323ljZFyS8
https://youtu.be/FZgrQP1UIBI
https://youtu.be/t2fJXjIYAkM
https://youtu.be/k9Oi4gwEheQ
https://youtu.be/5RNTmcJbeEo
https://youtu.be/tdH7OznLmxk
https://youtu.be/yjIr_0vf9-I
https://youtu.be/K6Fbu_FsXJo
https://youtu.be/3HYxX56ia8I
https://youtu.be/j3665aPsnbM
https://youtu.be/ynEKHdvD8R0

Formule
- f = \sqrt[N]{\prod\limits^N_{i=1}\left|\sqrt{(x-x_i)^2+(y-y_i)^2}-r_i\right|}
Cybernetic Kaleidoscope 1
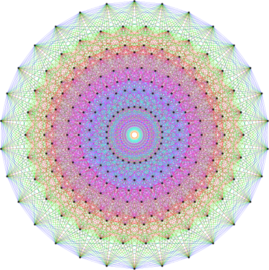
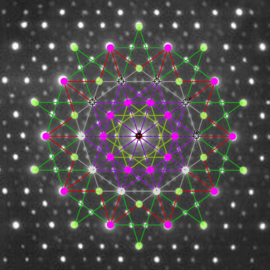
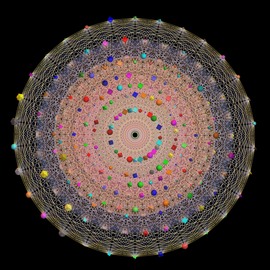
A superposition of many circles. The basic function for one circle is a cone with the apex pointing down and compressed up. The final function for N circles is the geometric mean value of N basic functions.

Cybernetic Kaleidoscope 2

Cybernetic Kaleidoscope 3

Cybernetic Kaleidoscope 4

Cybernetic Kaleidoscope 5

Cybernetic Kaleidoscope 6

Cybernetic Kaleidoscope 7

Cybernetic Kaleidoscope 8

Cybernetic Kaleidoscope 9

Formule
- \sqrt[N]{\prod\limits^N_{i=1}\left(\sqrt{(x-x_{i1})^2+(y-y_{i1})^2}+\sqrt{(x-x_{i2})^2+(y-y_{i2})^2}-\sqrt{(x_{i1}-x_{i2})^2+(y_{i1}-y_{i2})^2}\right)}
Cybernetic Star
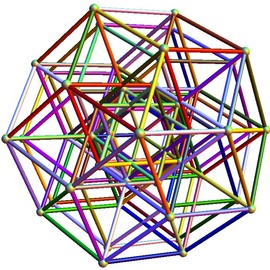
A superposition of several lines. The basic function for one line running from point 1 to point 2 consists of two cones with the apex pointing down at the position of point 1 and 2. The final function for N lines is the geometric mean value of N basic functions.

Cybernetic Flowers 1
Arcs are constructed by conformal mapping of circles on lines and using the line function of previous image. Again, several arcs are combined by taking the geometric mean value of the basic functions for single arcs.

Cybernetic Flowers 2

Formule
- f = \sum\limits^N_{i=1}\left( \frac{C}{\sqrt{(x-x_i)^2+(y-y_i)^2}} - \arctan\frac{ y-y_i }{ x-x_i } \right)

Cybernetic Helices 2

Cybernetic Polygons 1

Billowing Blueness

Formule
- f = C \cdot \sqrt{x^2+\left(y-a\right)^2} \cdot \sqrt{ x^2+\left(y+a\right)^2}
Interferences 1

Interferences 2
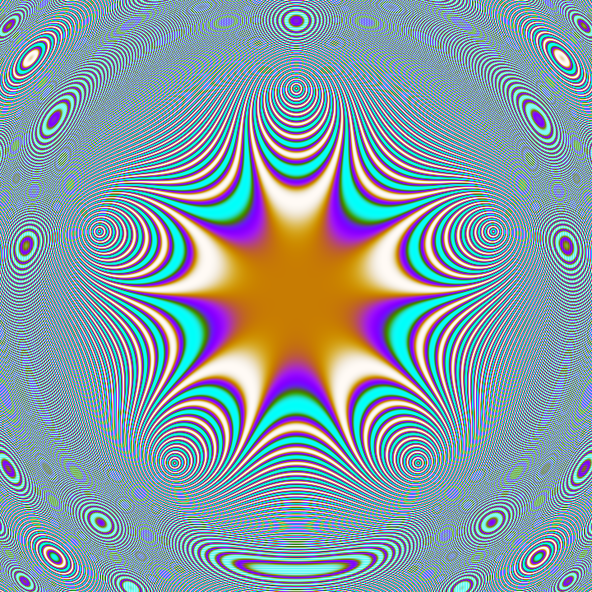
Interferences 3

Formule
- f = \sin(a \cdot x) \sin(b \cdot y) + \sin(c \cdot x) \sin(d \cdot y)
Cybernetic Billows 1

Cybernetic Billows 2

Cybernetic Billows 3

Formule
- f = \arctan\frac{y}{x} – a \cdot \sin(b \cdot \sqrt{x^2+y^2})
Cybernetic Billows 4

Cybernetic Billows 5

Cybernetic Billows 6

Cybernetic Billows 7

Cybernetic Billows 8

Cybernetic Polygons 2
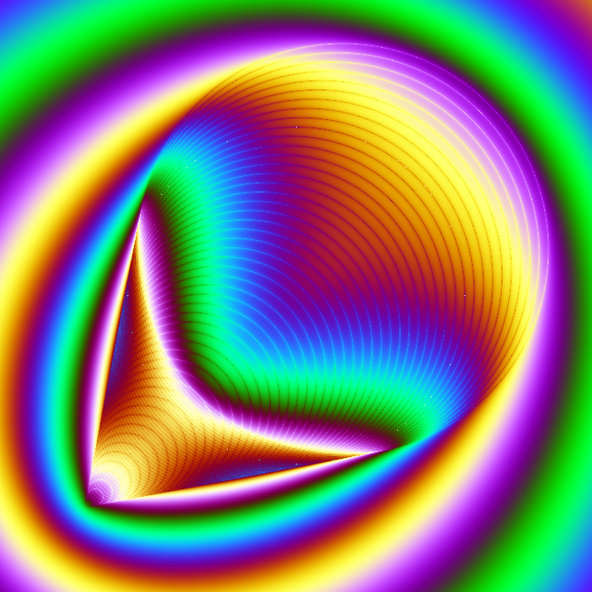
Cybernetic Comet

Cybernetic Kaleidoscope 10

Cybernetic Flower 3

Cybernetic Flower 4

Cybernetic Roller Bearings 1

Cybernetic Roller Bearings 2

Cybernetic Roller Bearings 3

Tasso