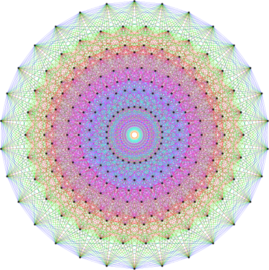
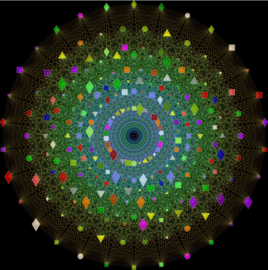
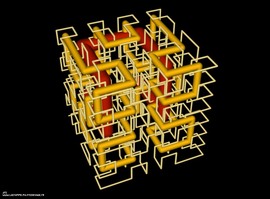
Some 2D Math Pictures
갤러리
Some 2D Math Pictures
Christian Gaier는 다채로운 기하학적 사진들과 영상들을 만드는 것이 취미입니다. 그는 기본적인 기하학적 대상(선,원,원호)들을 다채로운 배경에서 시각화 할 수 있는 수학적 함수들을 개발했습니다. 이 함수들은 더 많은 복잡한 기하학적 대상들을 만들기 위해 쉽게 합쳐질 수 있습니다. 함수들의 조합은 단순한 곱들로 간단히 재현될 수 있습니다. 이 그림 계산을 위한 소프트웨어들은 C언어로 작성되었습니다.

공식
- f = \sqrt[N]{\prod\limits^N_{i=1}\left|\sqrt{(x-x_i)^2+(y-y_i)^2}-r_i\right|}
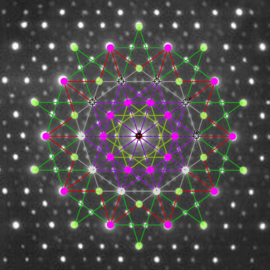
Cybernetic Kaleidoscope 1
수많은 원들이 중첩된 그림입니다. 하나의 원에 대한 기본 함수는 꼭지점이 아래를 향하고 압축된 원뿔입니다. N개의 원에 대한 최종 함수는 N개의 기본함수에 대한 기하평균입니다.
저작권 CC BY-NC-SA-3.0

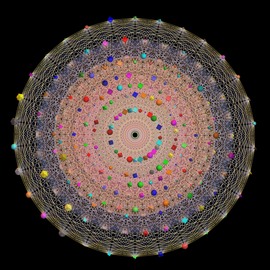
Cybernetic Kaleidoscope 2
저작권 CC BY-NC-SA-3.0

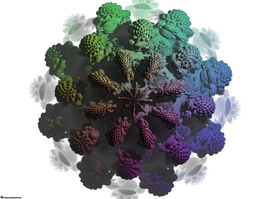
Cybernetic Kaleidoscope 3
저작권 CC BY-NC-SA-3.0

Cybernetic Kaleidoscope 4
저작권 CC BY-NC-SA-3.0

Cybernetic Kaleidoscope 5
저작권 CC BY-NC-SA-3.0

Cybernetic Kaleidoscope 6
저작권 CC BY-NC-SA-3.0

Cybernetic Kaleidoscope 7
저작권 CC BY-NC-SA-3.0

Cybernetic Kaleidoscope 8
저작권 CC BY-NC-SA-3.0

Cybernetic Kaleidoscope 9
저작권 CC BY-NC-SA-3.0

공식
- \sqrt[N]{\prod\limits^N_{i=1}\left(\sqrt{(x-x_{i1})^2+(y-y_{i1})^2}+\sqrt{(x-x_{i2})^2+(y-y_{i2})^2}-\sqrt{(x_{i1}-x_{i2})^2+(y_{i1}-y_{i2})^2}\right)}
Cybernetic Star
여러 선들의 중첩으로 만들어졌습니다. 점 1과 점 2를 잇는 직선의 기본함수는, 꼭지점이 각각 점 1, 2를 향하는 두 개의 원뿔로 이루집니다. N개의 직선에 대한 최종 함수는 이들 N개 기본함수의 기하평균으로 주어집니다.
저작권 CC BY-NC-SA-3.0

Cybernetic Flowers 1
그림의 호들은 원 위에서의 선들을 등각변환(conformal mapping) 시키고, 기존의 선의 함수들을 같이 사용해 얻어집니다. 역시 여러 개의 호들은, 이들의 기본 함수의 기하 평균을 취하는 과정에서 합쳐집니다.
저작권 CC BY-NC-SA-3.0

Cybernetic Flowers 2
저작권 CC BY-NC-SA-3.0

공식
- f = \sum\limits^N_{i=1}\left( \frac{C}{\sqrt{(x-x_i)^2+(y-y_i)^2}} - \arctan\frac{ y-y_i }{ x-x_i } \right)

Cybernetic Helices 2
저작권 CC BY-NC-SA-3.0

Cybernetic Polygons 1
저작권 CC BY-NC-SA-3.0

Billowing Blueness
저작권 CC BY-NC-SA-3.0

공식
- f = C \cdot \sqrt{x^2+\left(y-a\right)^2} \cdot \sqrt{ x^2+\left(y+a\right)^2}
Interferences 1
저작권 CC BY-NC-SA-3.0

Interferences 2
저작권 CC BY-NC-SA-3.0
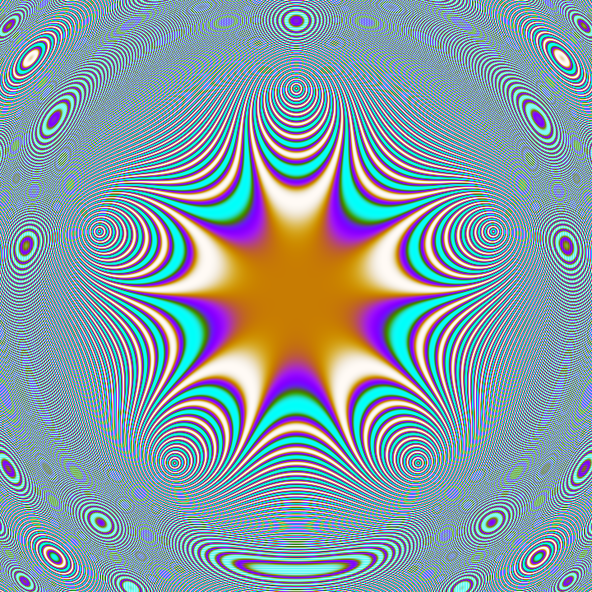
Interferences 3
저작권 CC BY-NC-SA-3.0

공식
- f = \sin(a \cdot x) \sin(b \cdot y) + \sin(c \cdot x) \sin(d \cdot y)
Cybernetic Billows 1
저작권 CC BY-NC-SA-3.0

Cybernetic Billows 2
저작권 CC BY-NC-SA-3.0

Cybernetic Billows 3
저작권 CC BY-NC-SA-3.0

공식
- f = \arctan\frac{y}{x} – a \cdot \sin(b \cdot \sqrt{x^2+y^2})
Cybernetic Billows 4
저작권 CC BY-NC-SA-3.0

Cybernetic Billows 5
저작권 CC BY-NC-SA-3.0

Cybernetic Billows 6
저작권 CC BY-NC-SA-3.0

Cybernetic Billows 7
저작권 CC BY-NC-SA-3.0

Cybernetic Billows 8
저작권 CC BY-NC-SA-3.0

Cybernetic Polygons 2
저작권 CC BY-NC-SA-3.0
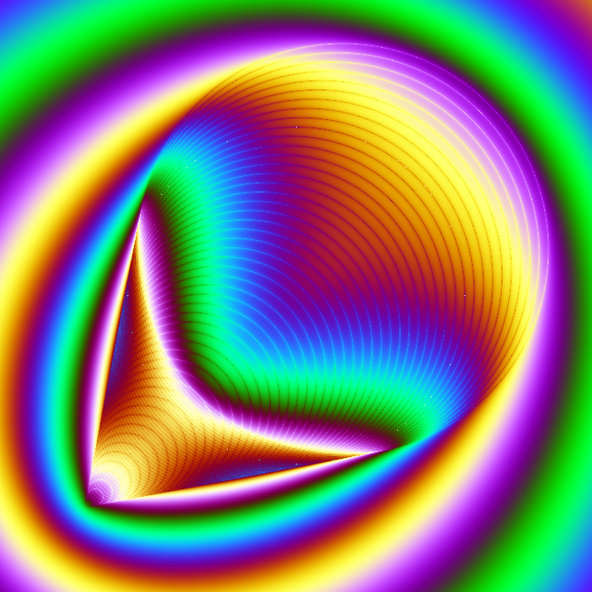
Cybernetic Comet
저작권 CC BY-NC-SA-3.0

Cybernetic Kaleidoscope 10
저작권 CC BY-NC-SA-3.0

Cybernetic Flower 3
저작권 CC BY-NC-SA-3.0

Cybernetic Flower 4
저작권 CC BY-NC-SA-3.0

Cybernetic Roller Bearings 1
저작권 CC BY-NC-SA-3.0

Cybernetic Roller Bearings 2
저작권 CC BY-NC-SA-3.0

Cybernetic Roller Bearings 3
저작권 CC BY-NC-SA-3.0

Tasso
저작권 CC BY-NC-SA-3.0

My Flower Painting Sister
저작권 CC BY-NC-SA-3.0