Ulrich Pinkall, Nicholas Schmitt, Charles Gunn and Tim Hoffmann
Differential geometry is the study of curved shapes, like curved lines or surfaces in space, or even shapes with many dimensions. From the viewpoint of differential geometry the shapes of soap films and soap bubbles are singled out by the fact that the so-called “mean curvature” is the same at every point of the surface. Several pictures in this gallery show surfaces of constant mean curvature, one picture shows a surface that does not have minimal area but minimal “total curvature”. Another picture shows a three dimensional space of constant curvature.
Discrete Minimal Surface
Minimal surfaces are a classical subject matter of differential geometry. They are surfaces whose mean curvature vanishes everywhere. The best known among this surface class are the Catenoid and the Helicoid. One of the many interesting features of minimal surfaces is the existence of an associated family. This means that the surfaces are deformed in such a way that they remain minimal (they are even isometrical to each other and corresponding tangent planes are parallel). Helicoid and Catenoid belong to the same associated family. As a result, they can be deformed into one another and in between surfaces are minimal, as well.
The image shows a discretization of the minimal surface half way between Catenoid and Helicoid. It is composed of spheres and circles touching each other at their points of contact. There is also an associated family for these discrete minimal surfaces and both the radii of corresponding spheres and the positions of corresponding circle disks are equal.
The scene was developed with jReality, the image itself was calculated by POV- Ray.
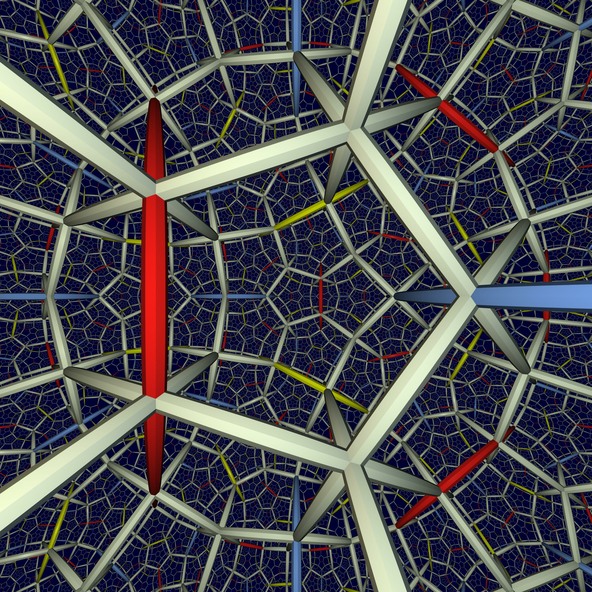
Hyperbolic Space
The image allows a look into the three-dimensional hyperbolic space as it is filled out by countless regular Dodocaeders. The hyperbolic space is a curved space namely with negative curvature. This means that as the distance grows it diverges more strongly than our flat space.
The surfaces of the Dodocaeder hit each other at right angles in the hyperbolic space what, however, cannot easily be seen due to our viewing habits adjusted to flat geometry. Just as in the case of the flat space being filled out by cubes here, as well, eight bodies obviously hit each other at their vertices.
The filling of the hyperbolic space by Dodocaeders shown above appears in topology if you try to geometrically realize the sur- rounding space of the so-called Borromean Rings. The red, yellow and blue beams in the image correspond to the three rings which cause this intertwining. The image shows the scenery such as an inhabitant of the hyperbolic space would conceive it. An attempt has even been made to adapt the lighting calculations to hyperbolic optics.
The scene was developed with jReality, the image itself was calculated by Renderman. Supported by DFG Research Centre Matheon.
Boy Surface
The Boy surface is generated by adding a moebius strip with a disk attached to its boundaries to a closed surface. The fact that this is made possible at all was proved by Werner Boy in 1901. The Boy surface intersects itself, but otherwise looks smooth in each of its points.
The version shown here is characterized by its mean curvature being as small as possible. It has “no unnecessary bumps“in this sense. Here, you see the most “beautiful“ possible realization of Boy surface in a mathematically precise sense. This is a parametrization of Boy surface by Robert Bryant and Robert Kusner.
The image is based on a bullet panorama which Paul Debevec generated from photos of a church in San Francisco. The scene was compiled in jReality, the image itself was calculated with Sunflow. Promoted by the DFG-Research Centre Matheon.
Helicoid with Handles
One of the best known minimal surfaces is the Helicoid which you know from your daily life of spiral staircases and parking ramps. It is, indeed, possible to connect different sheets of the Helikoid with each other without destroying the minimal surface feature or making that the surface starts intersecting itself. This connecting piece is called „handle“in mathematical terminology. Depending on which storey you are such a handle looks like a hole in the floor or ceiling, or even like a column which connect floor and ceiling of a storey. The surface shown (above) is a Helicoid with two handles and was found and calculated by Markus Schmies.
The image is based on a computer-generated landscape compiled using Terragen by Simon O’Callaghan. The scene was developed with jReality, the image itself was calculated by Sunflow. Promoted by the DFG Research Centre Forschungszentrum Matheon.
Bursting Nodoid
The bursting Nodoid is a special surface with constant mean curvature. Such a surface can be imagined as a boundary surface between two liquids or gases at different pressure such as a soap bubble enclosing a certain air volume. In contrast to physical soap bubbles mathematical soap bubbles are allowed to intersect themselves.
You have to imagine that all five extensions which you see emanating from the surface continue without end. And a balance of forces is achieved: The four undulated tubes draw the upper end down and thus keep the middle column pressing upward in balance.
The surface was developed by Nicholas Schmitt (GeometrieWerkstatt Tübingen) and he also designed and calculated the image using XLab software.
Tetranoid
The Tetranoid belongs to the class of surfaces which have the same curvature features as physical soap bubbles. Mathematically you say: The Tetranoid has a “constant mean curvature”. The four “legs“ of the Tetranoid are never ending, actually.
The existence of the Tetranoid (like the existence of similar surfaces with any symmetry based on the platonic bodies) was proved by Nicholas Schmitt, he also calculated the surface.
The image is based on a bullet panorama which Paul Bourke generated from photos. The scene was compiled in jReality, the image itself was calculated with Sunflow. Promoted by the DFG-Research Centre Matheon.
Twizzle Torus
The Twizzle Torus is an annular surface with a constant mean curvature in the three-dimensional sphere, a space curved in itself. To make it visible it must first be projected into our flat space. Luckily, this is enabled such that basic shape features can be maintained. In the three-dimensional sphere where it belongs to it has a screw symmetry which can still be surmised during projection.
The Twizzle Torus is only a comparatively simple example in an endless hierarchy of increasingly complex annular surfaces with similar curvature features.
The surface was developed by Nicholas Schmitt (GeometrieWerk- statt Tübingen) and he has designed and calculated the image using XLab software.
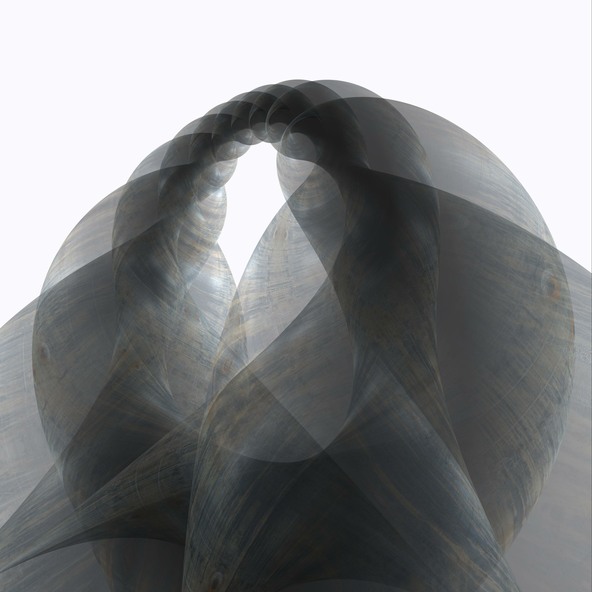
Björling Surface
Minimal surfaces are surfaces which have the same curvature features as physical soap films. The construction of minimal surfaces with given features is a classical subject of differential geometry. In 1844, E. G. Björling showed that for each sufficiently benign space curve a narrow minimal surface strip can be found which contains the curve. Furthermore, it can even be specified how the strip shall twist around the curve.
The surface shown here is generated with the basic curve as a Helix along which the strip is twisted at constant speed.
The formulas of this particular Björling surface come from Matthias Weber. The image is based on a computer generated landscape compiled using Terragen by Simon O’Callaghan. The scene was developed with jReality; the image itself was calculated by Sunflow. Supported by DFG-Research Centre Matheon.