Ulrich Pinkall, Nicholas Schmitt, Charles Gunn ve Tim Hoffmann
Diferansiyel geometri uzaydaki eğri çizgi ve yüzeyler gibi kavisli şekillerin ve hatta çok boyutlu şekillerin çalışıldığı bir alandır. Bir sabun katmanının ve baloncuğunun şekillerini düşünelim. Diferansiyel geometrinin bakış açısıyla, bu şekiller «ortalama eğrilik» (mean curvature) diye bilinen çokluğun bu yüzeylerin her noktasında aynı olması gerçeği sayesinde diğerlerinden ayrılır. Bu galeride «sabit ortalama eğriliğe» (constant mean curvature) sahip birçok görsel bulabilirsiniz. Örneğin bunlardan bir tanesi minimal alana sahip olmayıp minimal «toplam eğriliğe» sahip bir yüzeyi gösterirken, bir diğer görsel «sabit eğriliğe» (constant curvature) sahip üç boyutlu bir uzayı gösteriyor.
Ayrık Bir Minimal Yüzey
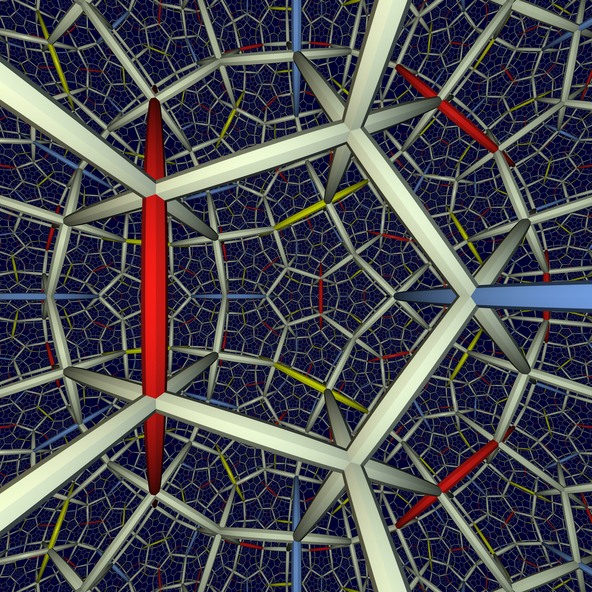
Hiperbolik Uzay
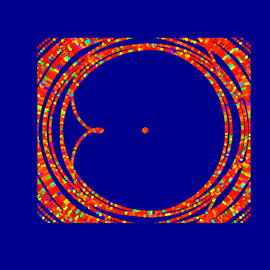
Buradaki resim, sayısız “düzgün onikiyüzlü” ile doldurulmuş üç boyutlu hiperbolik uzaya bakmamıza olanak sağlıyor. Hiperbolik uzaylar, negatif eğriliğe sahip eğri uzaylardır. Bu da, aynı yolu gittiğimizde, uzaklığın bizim düz uzayımızdan çok daha hızlı bir biçimde artması anlamına gelmektedir.
Onikiyüzlüler, hiperbolik uzayda birbirlerine doksan derece açıyla değer ancak düz geometriye ayarlı bizim kendi evrim kaynaklı algı alışkanlıklarımızla bu durum kolayca görülemez. Tıpkı düz uzayı dolduran küplerin altı tanesinin bir köşede birbirlerine dik dokunmaları gibi, burada da sekiz adet onikiyüzlü bariz bir şekilde birbirlerine köşelerinden dokunurlar.
İkişer ikişer birbirine geçmemiş ama üçü birbirine düğümlenmiş üç çemberden oluşan ünlü Borromean halkalarını çevreleyen uzay, 3 boyutlu hiperbolik uzay olarak görülebilir. Bunun, uzayı buradaki gibi onikiyüzlülerle doldurmakla yakından ilişkisi vardır. Resimdeki kırmızı, sarı ve mavi kenarlar, Borromean halkalarındaki o üç çembere denk gelir. Hiperbolik uzayda yaşayan biri uzayı bu resimdeki gibi algılayacaktı. Burada ışıklandırma hesapları dahi hiperbolik optiğe uygun olacak şekilde yapılmaya çalışılmıştır.
Bu sahne jReality ile derlenmiştir, cismin kendisi Renderman tarafından ışıklandırılmış ve renklendirilmiştir. Proje DFG Research Centre Matheon tarafından desteklenmiştir.
Boy Yüzeyi
Boy yüzeyi, bir daire ile bir Möbius şeridinin kenarlarından birbirine yapıştırılmasıyla elde edilen ve reel projektif düzlem denen yüzeyin 3 boyutlu uzaya yerleştirilmiş halidir. Bunun 3 boyutta mümkün olduğu gerçeği Alman matematikçi Werner Boy tarafından 1901 yılında kanıtlanmıştır. Boy yüzeyi kendisiyle kesişmekle birlikte tüm noktalarında tamamıyla pürüzsüz gözükür, tekillikleri yoktur.
Burada gösterilen halinde, ortalama eğriliği olabilecek en küçüktür. Üzerinde “gereksiz tümsekler” yoktur. Burada Boy yüzeyinin matematiksel kesinlik anlamında görüp görebileceğiniz en “güzel” halini görüyorsunuz. Bu biçim, Boy yüzeyinin Robert Bryant ve Robert Kusner tarafından keşfedilmiş bir parametrizasyonu aracılığıyla elde edilmiştir.
Resim, Paul Debevec’in San Francisco’daki bir kilisenin fotoğraflarından oluşturduğu panaromayı kullanıyor. Görsel jReality ile derlenmiş olup, cismin kendisi Sunflow ile tasarlanmıştır. Proje DFG-Research Centre Matheon tarafından desteklenmiştir.
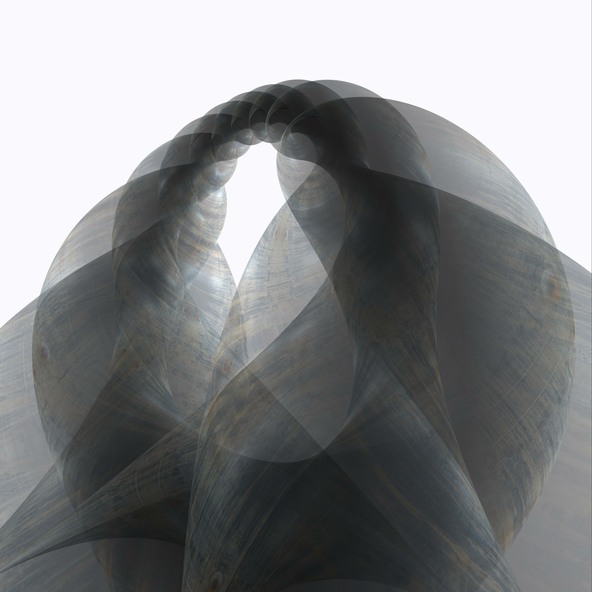
Kulplu helikoid
Günlük yaşamda spiral merdivenler ve otopark rampalarından bildiğiniz Helikoid, en çok bilinen minimal yüzeylerden bir tanesidir. Minimum yüzeye sahip olma özelliğini yok etmeden ve yüzeyin kendisiyle kesişmesine izin vermeden farklı Helikoid tabakalarını birbirine bağlamak da mümkündür. Bu bağlantı parçasına matematiksel terminolojide “Kulp” denir. Hangi katta olduğunuza bağlı olarak bu kulp, zeminde veya tavanda bir delik, hatta bir kattaki zemini ve tavanı birbirine bağlayan bir sütun gibi bile görünebilir. Burada gösterilen yüzey iki kulplu bir Helikoiddir ve Markus Schmies tarafından bulunup hesaplanmıştır.
Resim, Simon O’Callaghan tarafından Terragen kullanılarak tasarlanmış bir manzarayı fon olarak kullanıyor. Görsel, jReality ile geliştirilmiştir; Helikoid ise Sunflow ile tasarlanmıştır. Proje DFG Research Centre Forschungszentrum Matheon tarafından desteklenmiştir.
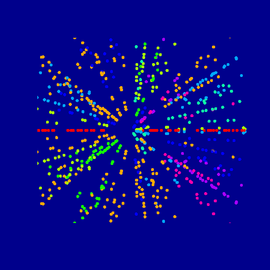
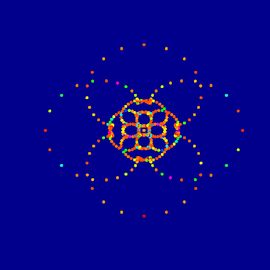
Bursting Nodoid
The bursting Nodoid is a special surface with constant mean curvature. Such a surface can be imagined as a boundary surface between two liquids or gases at different pressure such as a soap bubble enclosing a certain air volume. In contrast to physical soap bubbles mathematical soap bubbles are allowed to intersect themselves.
You have to imagine that all five extensions which you see emanating from the surface continue without end. And a balance of forces is achieved: The four undulated tubes draw the upper end down and thus keep the middle column pressing upward in balance.
The surface was developed by Nicholas Schmitt (GeometrieWerkstatt Tübingen) and he also designed and calculated the image using XLab software.
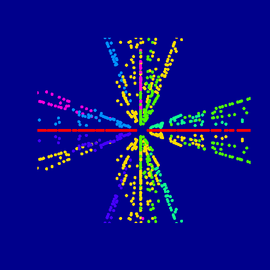
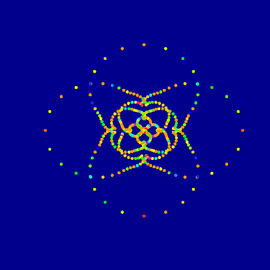
Tetranoid
The Tetranoid belongs to the class of surfaces which have the same curvature features as physical soap bubbles. Mathematically you say: The Tetranoid has a “constant mean curvature”. The four “legs“ of the Tetranoid are never ending, actually.
The existence of the Tetranoid (like the existence of similar surfaces with any symmetry based on the platonic bodies) was proved by Nicholas Schmitt, he also calculated the surface.
The image is based on a bullet panorama which Paul Bourke generated from photos. The scene was compiled in jReality, the image itself was calculated with Sunflow. Promoted by the DFG-Research Centre Matheon.
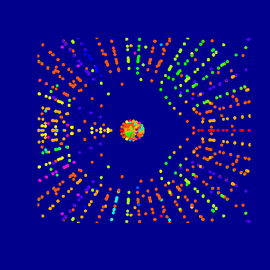
Dönen Simit
Dönen Simit, kendisi de eğri olan üç boyutlu kürede, sabit ortalama eğriliğe sahip halka biçimli bir yüzeydir. Bunu görünür kılmak için ilk önce üç boyutlu küreden bizim düz uzayımıza izdüşüm almak gerekir. Neyse ki bu izdüşüm şeklin temel özellikleri korunacak biçimde yapılabilir. Yüzey, bulunduğu üç boyutlu kürede, düz uzayımızda da gördüğümüz bir vida simetrisine sahiptir.
Benzer eğrilik özelliklerine sahip halka şeklindeki yüzeylerin oluşturduğu giderek daha karmaşıklaşan, sonsuz bir hiyerarşi içinde Dönen Simit nispeten basit bir örnektir.
Gördüğünüz yüzey Nicholas Schmitt (GeometrieWerk- statt Tübingen) tarafından geliştirilmiştir. Görüntünün tasarımı ve hesaplaması Xlab yazılımı kullanarak yapılmıştır.
Björling Yüzeyi
Minimal yüzeyler, sabun köpüğünün ince tabakasıyla aynı eğrilik özelliklerine sahip olan yüzeylerdir. Bu özelliklere sahip olan minimal yüzeylerin inşası, diferansiyel geometrinin önemli bir konusudur. 1844 yılında, İsveçli matematikçi E. G. Björling her makul uzay eğrisi için bu eğriyi içeren dar bir minimal şerit yüzey bulunabileceğini gösterdi. Hatta bu şeridin eğri etrafında nasıl büküleceği dahi belirlidir.
Burada gösterilen yüzey, mastar eğrimiz Sarmal (Helix) boyunca minimal şeridin sabit bir hızda bükülmesiyle elde edildi.
Bu özel Björling yüzeyinin formülleri Matthias Weber’e aittir. Bu görselin derlenmesinde, Simon O’Callaghan’ın ürettiği Terragen programıyla hazırlanan bir manzara resminden faydalanıldı. Görsel, jReality programıyla geliştirilirken, şeklin kendisi de Sunflow tarafından hesaplanarak oluşturuldu. Proje, DFG-Research Centre Matheon tarafından da desteklendi.