(3, 4, 5) 혹은 (4961, 6480, 8161) 같은 피타고라스 순서쌍(피타고라스 정리의 식인 a^2+b^2=c^2을 만족하는 정수의 순서쌍)들은 기원전 1600년전 경 고대 바빌로니아인들에게 잘 알려져 있었습니다. 그들은 또한 정수 변을 가지는 직각삼각형이 주어진 제곱수를 두 제곱수의 합으로 나타내는 문제와 대응됨을 알고 있었습니다. 이런 순서쌍이 기원전 300년전부터 자세히 연구되어 왔음에도 불구하고, 페르마(Pierre de Fermat)가 다음의 유명한 관찰 결과를 내놓은 것은 17세기 중반에 이르러서였습니다. “세제곱수는 두 개의 세제곱수로 나누어질 수 없으며, 네제곱수 역시 그러하고, 더 일반적으로 2 이상의 거듭제곱수는 같은 종류의 거듭제곱수의 합으로 나타낼 수 없다.”

“A^N+B^N=C^N 식에서 N이 2 이상일 때는 0이 아닌 정수해가 존재하지 않는다”는 이 관찰은 유명한 “페르마의 마지막 정리”가 되 었습니다. 이는 3세기 반이나 지난 1994년에 20세기 타원곡선 이론을 사용하여 완전히 증명되었습니다.

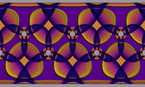
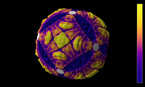
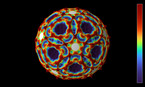
타원곡선은 깊고 아름다운 성질을 갖습니다. 이는 19세기 즈음부터 연구되어 온 y2 = x3 + a·x + b 라는 형태로 표현되는 평면곡선입니다. 아핀 평면(affine plane)서의 이 방정식은 동차방정식 y2 z= x3 + a·xz2 + b·z3 에 대응되고, 이는 공간에서 두 개의 변수 a,b 를 갖는 대수곡면의 모임을 나타냅니다. 이 식을 변형시켜 우리 상상력과 수학적 창의성을 자극하는 애니메이션을 만들 수 있습니다. 

암호학은 비밀 혹은 귀중한 정보를 전송하고 보호하는 안전한 방법을 일컫습니다. 1977년부터 널리 사용된 RSA 공개 키 방식은 소수의 이론과 매우 큰 정수의 인수분해를 이용하여 만들어졌습니다. 타원 곡선 방법론이 정수의 인수분해에 미친 지대한 영향 덕분에 타원 곡선 암호(ECC)가 1985년 수학자들에 의해 고안되었고, 그 이후 암호학에서의 수학적 정교함은 새로운 단계로 발전하였습니다.

ECC 알고리즘의 보안은 타원 곡선의 이산 로그(discrete logarithm) 문제에 기초하고, 이는 유한체(finite filed) 연산에서는 더 어려운 문제처럼 보일 수도 있습니다. 근래의 수학적 발전은 ECC에서는 비교적 작은 크기의 키로 충분한 보안 수준을 보장할 수 있다는 것을 말해줍니다. 예를 들어 160 비트의 ECC 키는 1024 비트 RSA 키와 비슷한 보안 수준을 만들어 냅니다.

타원 곡선 이론은 정수론, 대수학과 기하학 간의 연관성의 아름다움을 보여주며, 전자상 거래나 통신 보안을 강화하는데 강력한 수학적 툴을 제공합니다. 카이사르 암호는 d = c - 3 (mod 26) 와 같은 단순 사칙연산만 사용하는데 이는 구식입니다. 그러나 이는 이 영상의 제목을 해독하는 열쇠입니다. (역주: 제목의 알파벳 글자들을 3칸만큼 앞으로 옮겨 보세요.

영상은 아래의 링크에서 다운받을 수 있습니다. (포르투갈어, 독일어, 영어 그리고 스페인어 지원)

http://www. cim.pt/LPD-UHW