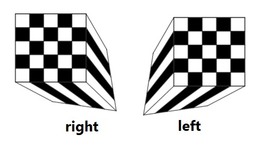
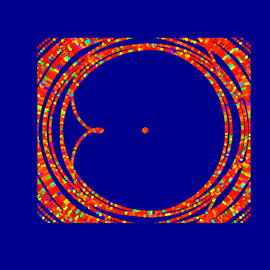
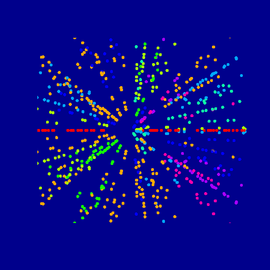
jReality Screenshots
프로그램 jReality의 스크린샷입니다.

Matheon 곰
Matheon 수학연구소(DFG-Forschungszentrum Matheon)의 곰 조각상은 베를린 공과대학(Technische Universität Berlin)의 수학과 건물 앞에 높여 있습니다. 곰 조각상 위의 무늬는 수학적 관점에서 매우 흥미롭습니다. 이는 Matheon 로고와 원으로 구성된 평면을 채우는 주기적 패턴을 바탕으로 만들어졌습니다. 여기서 수학적 과제는 이 패턴을 곰의 표면에 표현할 때 최대한 왜곡이 덜 잃어나게 하는 것입니다. 사실 패턴에서 나타나는 각을 곰 위에서도 그대로 볼 수 있고, 따라서 곰 위의 패턴의 상이 등각(conformal)이라 할 수 있습니다.

슈바르츠(Schwarz)의 최소곡면
극소곡면 혹은 최소곡면(minimal surface)은 비누막의 곡률의 물리학적 특징처럼, 곡률이 정해지는 곡면입니다. 여기 보이는 곡면은 수학자 슈바르츠(Karl Hermann Amandus Schwarz)에 의해 19세기에 발견되었고, 공간을 결정 격자처럼 주기적으로 채운다는 특징을 갖고 있습니다. 여러분이 보고 있는 것은 엄밀히 말하자면 부드러운 곡면은 전혀 아니고, 그저 서로 접하고 있는 원들로 이루어진 도형일 뿐입니다. 부드러운 곡면을 이렇게 “이산화(discretization)”하는 작업은, 최근의 건축에서 평평한 물체들로 이런 굽은 곡면을 만드는 데에 매우 중요하게 사용됩니다.

극소곡면 장소
여기서 보시는 것은 에네퍼(Enneper) 곡면의 하단에 배관 모양의 뻗어나온 가지 둘을 붙인 모습입니다.
무한히 뻗어나가면서 자기교차하지 않는 경계 없는 극소곡면을 만드는 데에는 매우 섬세한 기술이 필요합니다. 우선 이 곡면 조각은 끝없이 연장할 수 있으므로, 무한히 뻗어나간다는 요구조건은 만족됩니다. 하지만 곧 자기교차가 발생하게 됩니다. 이 점에서 본다면 이 곡면은 위에서 만족한 극소곡면을 만들기 위한 연습에서 나온 시행착오라고 볼 수도 있겠지만, 그럼에도 불구하고 매우 아름답습니다.

Willmore 토러스
비누막은 늘이는 힘에 대해 저항하는 소재로 이루어져 있지만, 원하는 방향으로 힘들이지 않고 굽힐 수 있습니다. 이와 대조되게 Willmore 곡면들은, 늘이는 힘에 대해 저항하지 않지만 굽히는 힘에 대한 탄성력이 작용하는 물질로 이루어져 있습니다. 여기 보이는 도형은 이 Willmore 특성을 갖고 있는 닫힌 토러스(torus)로서, Babich와 Bobenko의 이론을 바탕으로 Matthias에 의해 발견되었습니다.

테트라노이드
테트라노이드(Tetranoid)는 곡률이 비누막의 특징을 갖는 곡면들 중의 일부입니다. 수학적으로 이는 상수 평균 곡률을 갖고 있다고 할 수 있습니다. 테트라노이드의 네 “다리”들은 사실 끝이 없이 뻗어나갑니다. 수학자 Nicholas Schmitt는 테트라노이드처럼 정다면체의 대칭을 갖는 비슷한 곡면들의 존재성을 증명하였고 이들을 직접 계산해 내었습니다.

손잡이가 있는 나선면(helicoid)
흔히 나선 계단이나 주차장 진입 경사로등에서 볼 수 있는 나선면(helicoid)은 잘 알려진 극소곡면 중 하나입니다. 한편 이 나선면의 다른 층들을 자기교차 없이 연결하면서 여전히 극소곡면이 되게 하는 것이 가능합니다. 이 때의 연결 조각들은 수학적으로 “손잡이(handle)”이라고 불립니다. 바라보는 관점에 따라서 손잡이는 바닥 또는 천장의 구멍이나, 층 사이를 잇는 기둥처럼 보일 수 있습니다. 이 손잡이가 둘인 곡면은 Markus Schmies가 발견하고 계산해 내었습니다.

보이(Boy)의 곡면
보이(Boy)의 곡면은 뫼비우스 띠의 경계에 원판의 경계를 붙여서 만들어집니다. 이 조작이 부드럽게 가능하다는 것은 수학자 Werner Boy가 1903년에 증명하였습니다. 보이의 곡면은 자기교차하는 것을 제외하고는 각 점에서 부드러운(smooth) 형태를 갖습니다. 여기 보이는 형태는 이 중 평균곡률(mean curvature)이 최소화되는, 즉 “불필요한 돌출이 없는” 특성을 갖고 있습니다. 따라서 이는 보이 곡면의 가장 “아름다운” 표현이라는 것을 수학적으로 ‘정확하게’ 이야기할 수 있는 것입니다. 이 매개화는 Robert Bryant와 Robert Kusner가 찾아냈습니다.